FG-Squircular Mapping

The elliptical grid mapping is by no means the only way to map the square to a circle and vice versa.
In this entry, I shall introduce a disc to square mapping based on the Fernandez-Guasti squircle.

Here are the equations for the mapping.

square to circle:
u = x √(x² + y² - x²y²) / √(x² + y²)
v = y √(x² + y² - x²y²) / √(x² + y²)

circle to square:
x = √½  sgn(uv)/v √(u² + v² - √(u² + v²) √(u² + v² - 4u²v²) )
y = √½  sgn(uv)/u √(u² + v² - √(u² + v²) √(u² + v² - 4u²v²) )


where sgn(z) is the signum function;
(u,v) are circular coordinates in the domain {(u,v) | u² + v² ≤ 1}
(x,y) are square coordinates in the range [-1,1] x [-1,1]

Note: We need to handle zero inputs as a special case.
When input u or v is zero, just set x = u and y = v.
When input x or y is zero, just set u = x and v = y.

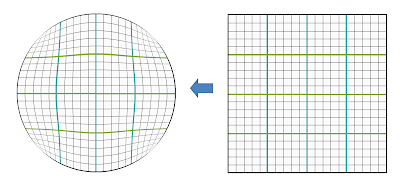
The main idea behind this mapping is to map concentric circles inside the circular disc to Fernandez-Guasti squircles inside the square.

See http://squircular.blogspot.com/2015/09/fernandez-guastis-squircle.html for more details on the Fernandez-Guasti squircle.

C++ sample implementation below
--------------------------------------------------------------------------------------------------

// sample code accompanying the paper:
// "Analytical Methods for Squaring the Disc"
// http://arxiv.org/abs/1509.06344

#include <stdio.h>
#include <math.h>

#define epsilon 0.0000001

inline double sgn(double input)
{
    double output = 1.0;
    if (input < 0.0) {
        output = -1.0;
    }
    return output;
}


// FG-Squircular mapping
// mapping a circular disc to a square region
// input: (u,v) coordinates in the circle
// output: (x,y) coordinates in the square
void fgsDiscToSquare(double u, double v, double& x, double& y)
{
    x = u;
    y = v;
 
    double u2 = u * u;
    double v2 = v * v;
    double r2 = u2 + v2;
    double uv = u * v;
    double fouru2v2 = 4.0 * uv * uv;
    double rad = r2 * (r2 - fouru2v2);
    double sgnuv = sgn(uv);
    double sqrto = sqrt(0.5 * (r2 - sqrt(rad)));

     if  (fabs(u) > epsilon)   {
        y = sgnuv/u * sqrto;
    }
   
    if  (fabs(v) > epsilon) {
       x = sgnuv/v * sqrto;
    }
 }


// FG-Squircular mapping
// mapping a square region to a circular disc
// input: (x,y) coordinates in the square
// output: (u,v) coordinates in the circle
void fgsSquareToDisc(double x, double y, double& u, double& v)
{
    u = x;
    v = y;
   
    double x2 = x * x;
    double y2 = y * y;
    double r2 = x2 + y2;
    double rad = sqrt( r2 - x2 * y2);

    // avoid division by zero if (x,y) is closed to origin
    if (r2 < epsilon)   {
        return;
    }

    // This code is amenable to the fast reciprocal sqrt floating point trick
    // https://en.wikipedia.org/wiki/Fast_inverse_square_root
    double reciprocalSqrt =  1.0/sqrt(r2);
 
    u = x * rad * reciprocalSqrt;
    v = y * rad * reciprocalSqrt;
}


int main()
{
    double x,y;
    double u,v;

    fgsSquareToDisc(0.0,-0.789,u,v);
    fgsDiscToSquare(u,v,x,y);
 
    printf("%f %f\n",u,v);
    printf("%f %f\n",x,y);

    fgsDiscToSquare(-0.31415, -0.926535,x,y);
    fgsSquareToDisc(x,y,u,v);
 
    printf("%f %f\n",x,y);
    printf("%f %f\n",u,v);

    return 0;
}